Golden: Phi, phi, and the Fibonacci Sequence
Two irrational numbers that perfectly play off of each other. A numerical sequence that nature follows everywhere. Things that make you go, “Hmmm.”
Pi — π or 3.14159… is an irrational number (the number of its decimal places goes on infinitely). Most people have heard of it in geometry class for calculations involving a circle (its radius and diameter).
It has two irrational cousins:
- Phi — ϕ or 1.61803…
- phi — φ or 0.61803…
Why is one the upper-case version and the other lower-case? Before we answer that, let’s take a look at the Fibonacci Sequence. The sequence itself is:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, etc.
To get the sequence, add two sequential numbers. Their sum is the next number in the sequence. So, we start with zero (0), the numeral that represents nothing or a void. The key is one (1), the numeral that represents wholeness and unity. Add one to zero, and the sequence begins.



This is the sequence that occurs in nature. The number of spirals of sunflowers and pineapples is tied to that sequence. It is also the basis for other designs in nature, including what we find attractive in the human face and the human form. It happens all around us. This is known as the “Golden Mean.”


What does this have to do with Phi and phi? Why is one spelled with a capital (and upper-case Greek letter) and the other not (and lower-case Greek letter)? Take a closer look at them:
- Phi = ϕ = 1.61803…
- phi = φ = 0.61803…
Phi begins with 1 and phi begins with 0. After the decimal point, they are both the same.
Now comes the interesting stuff:
- phi = Phi – 1
- Phi = phi + 1
- Phi = 1/phi
x = 1/x + 1 is known as the “Golden Ratio.”
Pretty cool, eh? Now look at this:
- Phi = (√5 + 1)/2 = 1.618…
- phi = (√5 – 1)/2 = 0.618…
As Mr. Spock would say, “Fascinating.” But wait! There’s more! Remember the Fibonacci Sequence? Starting around 34 and 55, as you go higher up the sequence, the results become freaky. Get a load of this:
34/55 = 0.618 = φ
55/34 = 1.618 = ϕ
55/89 = 0.618 = φ
89/55 = 1.618 = ϕ
. . . and that happens for every pair of numbers after that in the sequence! [queue the theme to “Twilight Zone” here]
There are those who say that everything in nature is not by design, but by coincidence. Politely speaking, I find that difficult to believe. One aspect of one type of lifeform—say, the disk flowers (dark center) of composite flowers (for example, sunflowers)—following the same mathematical progression (and a somewhat complicated one, as opposed to 1, 2, 3, 4, 5) is cool enough. But so many different things of so many different lifeforms and patterns throughout the universe?
- Disk flowers (e.g., sunflowers)
- Seeds (e.g., pine cones)
- Petals (e.g., roses)
- Leaves (e.g., aloe)
- Shells (various aquatic animals)
- Fetuses (various animals)
- Eggs (various birds)
- Hurricanes
- Galaxies
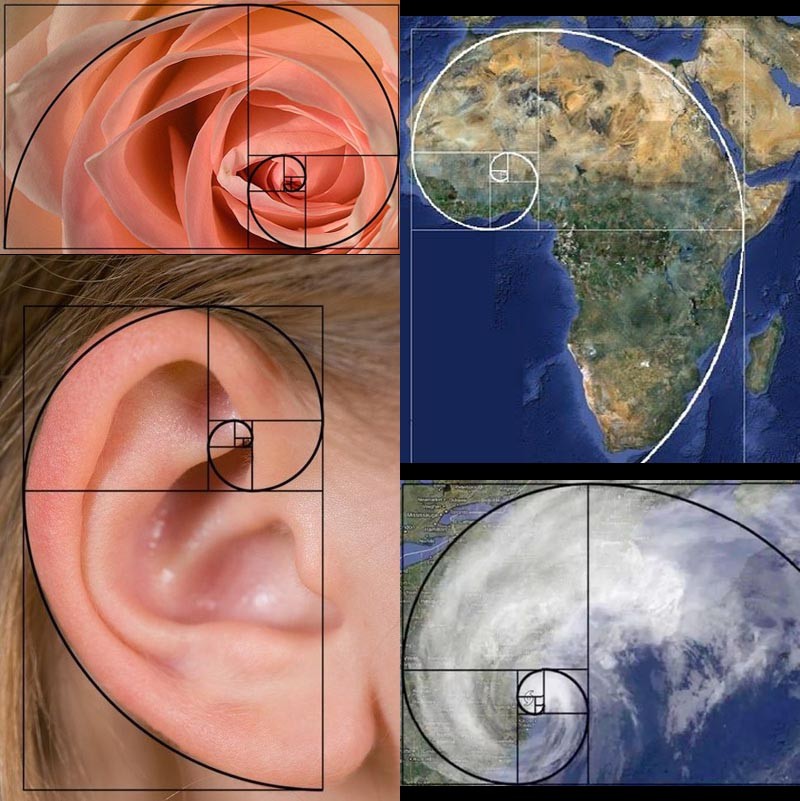
That’s not a string of coincidences. That’s a pattern. All of Creation follows a blueprint.
Moreover, to show that the ancient pyramids weren’t just coincidental designs, see how the Fibonacci spiral relates to the short and tall pyramid shapes:
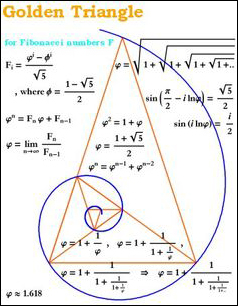
I love you and I thank you. Namasté.
